The rules are simple. The game isnt.
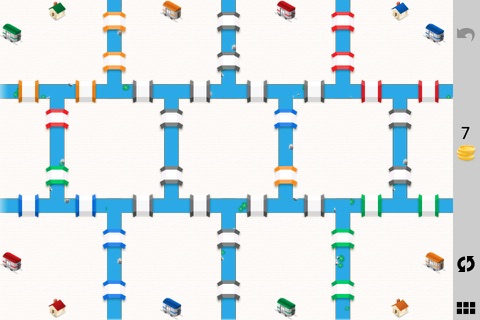
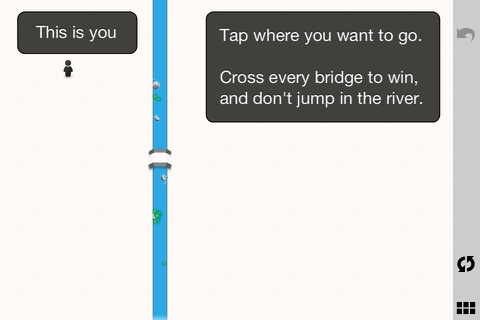
Youre visiting towns full of rivers. The rivers form islands with bridges connecting them. To beat the game just cross every bridge once and only once.
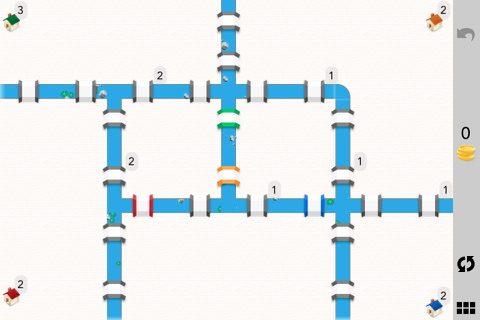
Each town challenges and entertains you with twists, turns, and a little man walking across bridges. The towns start simple and add more and more with houses to visit, colored bridges, tolls, and subways.
Seven Bridges comes with 80 towns and more on the way. The towns start off easy, build slowly, and end with a few tough ones.
Seven Bridges is a fun way to exercise your brain and perfect way to pass the time in boring meetings or the train ride home. Its also all open source. You can try it out for free, see the code, and take the whole game apart.
The Seven Bridges of Konigsberg
The city of Konigsberg in Prussia (now Kaliningrad, Russia) was built around two rivers with seven bridges. For years the residents tried to cross each bridge without crossing any of them more than once.
Leonhard Euler proved that it was impossible to cross all the bridges without repeating and laid the foundation for graph theory and modern topology at the same time.
This project is an iPad and iPhone game based on those famous bridges. Each level presents a puzzle with bridges to cross, houses to visit, and sometimes coins to collect.
Seven Bridges
Hot issue on graph theory research. The early 18th century Prussian Konigsberg, a river runs through, on two islands in the river, there are seven bridges the two islands and riparian. Individuals presented a problem: how a Pacers can not repeat missing time to finish the seven bridges, and finally back to the starting point of great mathematician Leonhard Euler later it into a geometric problem - a stroke. He not only solve this problem, and shows the connected graph can be a stroke important condition is that they are connected, and odd vertex (arc through this point, the number is odd), the number is 0 or 2.